Continuous function (set theory)

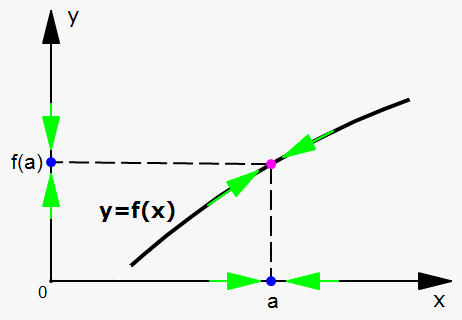
In set theory, a continuous function is a sequence of ordinals such that the values assumed at limit stages are the limits (limit suprema and limit infima) of all values at previous stages. More formally, let γ be an ordinal, and ${\displaystyle s:=\langle s_{\alpha }|\alpha <\gamma \rangle }$ be a γ-sequence of ordinals. Then s is continuous if at every limit ordinal β < γ,

${\displaystyle s_{\beta }=\limsup\{s_{\alpha }:\alpha <\beta \}=\inf\{\sup\{s_{\alpha }:\delta \leq \alpha <\beta \}:\delta <\beta \}}$

and

${\displaystyle s_{\beta }=\liminf\{s_{\alpha }:\alpha <\beta \}=\sup\{\inf\{s_{\alpha }:\delta \leq \alpha <\beta \}:\delta <\beta \}\,.}$

Alternatively, if s is an increasing function then s is continuous if s: γ → range(s) is a continuous function when the sets are each equipped with the order topology. These continuous functions are often used in cofinalities and cardinal numbers.

A normal function is a function that is both continuous and strictly increasing.

References